Scoperta l’equazione de “La Musica delle Sfere” del Sistema Solare: simmetrie speculari e scale musicali. Ad individuarla Nicola Scafetta, docente del Dipartimento di Scienze della Terra, dell’Ambiente e delle Risorse (DISTAR) dell’Università di Napoli Federico II con un lavoro pubblicato sulla rivista Frontiers in Astronomy and Space Sciences.
Lo studio che si inserisce nell’ambito della ricerca delle armonie del sistema solare noto sin dai tempi di Pitagora e Keplero come “La Musica delle Sfere”, osserva che una caratteristica peculiare del Sistema Solare è la sua architettura a riflessione speculare rispetto alla Cintura degli Asteroidi tra Marte e Giove. Questa architettura è composta da quattro pianeti terrestri interni (Mercurio, Venere, Terra e Marte) e quattro pianeti giganti gassosi esterni (Giove, Saturno, Urano e Nettuno) separati, per l’appunto, dalla Cintura degli Asteroidi.
Altri sistemi planetari, come ad esempio Sistema Solare Trappist-1, presentano una notevole sincronizzazione tra le varie orbite planetarie, ma nessun altro sistema esoplanetario simile al nostro è stato scoperto, e nessuno è stato in grado fino ad ora di determinare se l’architettura del Sistema Solare corrispondesse ad un ordine matematico preciso, nonostante studiosi del calibro di Pitagora e Keplero lo avessero sempre supposto.
Adottando una metrica ispirata alle scale musicali sviluppate dai tempi di Pitagora ad oggi, lo studio evidenzia una relazione matematica precisa fatta di simmetrie a specchio che lega tra di loro con un fattore di scala tutti i pianeti e le varie cinture di asteroidi e comete, e che è in grado di descrive l’intera distribuzione delle masse di tutto il disco planetario dal Sole fino al bordo più esterno del sistema solare. Inoltre, ogni orbita planetaria è legata a quella successiva con dei rapporti spaziali che corrispondono alle consonanti musicali.
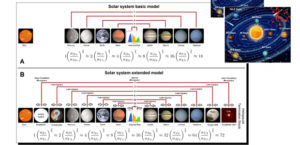
In base allo studio, ad ogni orbita planetaria ne corrisponde un’altra speculare alla Cintura degli Asteroidi. Si hanno cioè le seguenti coppie: Giove-Marte, Saturno-Terra, Urano-Venere, Nettuno-Mercurio, ed altre che coinvolgono gli anelli di asteroidi e comete. Per ogni coppia, il rapporto tra i raggi delle orbite dei due pianeti, quando elevato alla potenza di 2/3 (da non confondere con l’esponente usato nella terza legge di Keplero che è 3/2) è due volte più grande del rapporto relativo alla copia planetaria adiacente interna. In questo modo si genera un rapporto di scala (1, 2, 4, 8, ecc.) tra le coppie planetarie speculari e concentriche alla Cintura degli Asteroidi (vedi la Figura). Questi rapporti corrispondono a successive ottave nella scala musicale.
Inoltre, il rapporto fondamentale della scala planetaria è 9/8. Esso corrisponde ad una nota musicale, cioè, ad esempio, al rapporto tra le frequenze di un Re e un Do nella scala musicale. Il rapporto 9/8 è importante nella storia della matematica e della musica perché è l’epogdoon pitagorico che fu ritratto anche da Raffaelo in un famoso dettaglio de La Scuola di Atene.
L’equazione complessiva ha una precisione del 99%, è molto facile da ricordare ed è suggestiva di un ordine planetario. Essa descrive completamente la distribuzione delle masse del sistema solare e ha una chiara interpretazione musicale dimostrando così che Pitagora e Keplero erano nel giusto nel ritenere che il sistema solare fosse caratterizzato da una “Musica delle Sfere”.
...continua sulla fonte https://ift.tt/YdrefuO che ringraziamo.
Commenti
Posta un commento